Coordinates and Transformations
p5.js is a powerful tool for creating 2D graphics but it's also capable of 3D graphics. This tutorial will introduce new concepts for creating 3D sketches with p5.js.
Table of Contents
What is WebGL?
WebGL is a library that gives us the tools we need to create 3D graphics within a web browser. To put it simply, it allows us to do all kinds of math to help arrange and display objects in 3D. p5.js makes it easier to work with WebGL through its special WebGL mode.
Working in 3D introduces a lot of complexity, especially when a sketch involves motion, texture, lighting, and more. Luckily for us, computers have special hardware that is particularly well suited to performing those calculations, the graphics processing unit (GPU). The GPU is capable of processing many things simultaneously, which is especially important when we're dealing with pixels and many shapes in space.
Let's get started by setting up the p5.js to use WebGL, by passing WEBGL as a third parameter into createCanvas().
function setup() {
createCanvas(windowWidth, windowHeight, WEBGL);
describe('a red box on a white background');
}
function draw(){
background(255);
fill(255,0,0);
box();
}
3D Coordinate Space: Positioning in 3D
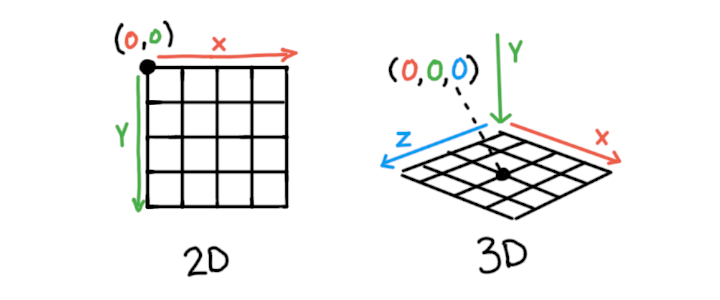
One of the most fundamental differences between working in 2D and working in 3D is the most obvious: there is one more dimension to work with. In addition to the horizontal and vertical position (x and y axes) of an element in our drawing, 3D adds depth, the z-axis.
When drawing in 2D, the point (0,0) is located at the top left corner of the screen. In WebGL mode, the origin of the sketch (0,0,0) is located in the middle of the screen. By default, the x-axis goes left-to-right, y-axis goes up-to-down, and the z-axis goes from further-to-closer.
Transformations: Position and Size of 3D Shapes
p5.js has a few methods, translate(), rotate(), and scale(), that we can use to position and orient objects within space. Each of these methods affect what is known as the model matrix. Collectively these are known as the transformation of an object. These methods are available for both 2D and 3D drawing.
translate(): Moving Objects in Space
translate() moves the origin in a given direction. Anything drawn after we call translate() will be positioned relative to that point. translate() accepts arguments for x, y, and z values. Use the sliders in the sketch above to change the translation of the box and see how it moves along each axis. The code below demonstrates simple translation on a box() shape.
...
// draw a box 100 units to the right
translate(100,0,0);
box();
..
rotate(): Orienting Objects in Space
rotate() reorients whatever is drawn after it.
There are a few methods that can be used to rotate an object in 3D. Most of the time it's easiest to call methods like rotateX(), rotateY(), and rotateZ() , which each allow for rotation around a specific axis. Each of these methods accept a single argument specifying the angle of rotation. Try moving the sliders in the example above to see how rotation is performed on each axis. The code below shows each of these methods in use.
...
// rotate X, Y, and Z axes by 45 degrees
rotateX(QUARTER_PI);
rotateY(QUARTER_PI);
rotateZ(QUARTER_PI);
box();
..
By default p5.js will expect angles to be in radians. Radians use numbers from 0 - TWO_PI to specify an angle. To use degrees, either convert degrees to radians using radians(), or use angleMode(DEGREES).
...
// rotate each axis by 45 degrees
rotateX(radians(45));
box();
//or
angleMode(DEGREES);
rotateY(45);
box();
..
You can also use rotate() , which allows you to specify which axis you'd like to rotate around using a vector as the second argument.
scale(): Size in Space
scale() changes the size of whatever is drawn after it. Like the other methods described so far, it accepts arguments for x, y, and z values.
The Order of Transformations Matters!
Something that can feel unpredictable at first is the order of transformations. Each transformation always affects the next one. For example, if rotate() is called, followed by translate(), the direction of that translation will be affected by the rotation. The entire coordinate system is rotating and moving, not just the shape itself.
Transformations can be performed in any order, but using translate, rotate, and then scale will be the most intuitive. Translation, followed by rotation, produces the effect of moving the shape and then rotating around that new location.
In the below example, try changing the order of translate() and rotateY() and see how it affects where the object is drawn.
p5.js also has some methods that can control when transformations are applied: push() and pop() . push() and pop() make it easier to move objects individually. The push() method saves the current transformations and style settings. Then, after performing new transformations, the pop() method is used to restore us to the the original transformations. The result is that whatever transformations or styling changes that are made between push() and pop() are isolated to that portion of the code. If you don’t use push() and pop(), you have to keep track of whatever transformations have already taken place, which can get complicated and difficult to follow. Consider this following example, which places two boxes in our sketch. To position the second box without push() and pop(), you have to account for the first transformation. This can be a lot to keep track of in a more complex 3D scene.
// draw a box 100 units to the right
translate(100,0,0);
box();
// now, to draw another box 100 units to the left
// since transformations accumulate, we have to
// subtract 200 to do this
translate(-200,0,0);
box();
Now, let's try the same code with push() and pop(). Now we can just translate the object where we want it, without having to remember where our coordinate system lies.
push(); // detach our coordinate system
// draw a box 100 units to the right
translate(100,0,0);
box();
pop(); // return to our original coordinate system
push(); // detach our coordinate system
// draw a box 100 units to the left
translate(-100,0,0);
box();
pop(); // return to our original coordinate system
While this is a more advanced topic, each of these transformations affect what is called the model matrix. The transformation matrix is combined with the view matrix and the projection matrix, both of which help simulate the view of a camera, and this combination results in our 3D scene!
Learn more about Model View ProjectionIn the below example, try removing push() and pop() to see how the transformations affect the second object that is drawn.
Basic Shapes in 3D
So far we have only been using box() but p5.js has seven different predefined geometries that you can use in your sketch. These basic predefined geometries are often referred to as 'primitives'.

These primitive shape methods are: box(), plane(), sphere(), ellipsoid(), cone(), cylinder(), and torus().
It is also possible to create custom geometry, either from scratch or from 3D models created in another program. More information about custom geometry can be found in the Custom Geometry tutorial .
Conclusion
By having basic control over a 3D coordinate space, transformations, and basic shapes, you should be able to begin creating basic scenes in 3D. The tutorials that follow this in the Getting Started in WebGL series will introduce custom geometries, allow you to tweak the appearance of the scene, and introduce you to some basic shader programming to push your sketches further.
Other Tutorials
This tutorial is part of a series about the basics of using WebGL in p5.js. Check out each of these other tutorials below.
- Coordinates and Transformations (you are here)
- Creating Custom Geometry in WebGL
- Styling and Appearance
- Introduction to Shaders
Glossary
GPU
The GPU (Graphics Processing Unit) is a piece of hardware that is particularly well suited for performing many calculations in parallel, making it powerful for 3D graphics.
Model
A custom 3D geometry that can be saved and loaded from a file.
Matrix
A special array that can hold information about the transformation of a geometry.
Camera
The viewpoint of a 3D scene.
Transform
Also referred to as transformation, this refers to the combined scale, rotation, and translation of a geometry.
Vertex
A point in 3D space, with an x, y, z position.
Face
A collection of three points that create a solid surface.
